Nous allons voir comment Généatique permet de créer des conditions complexes, par exemple pour la mise en valeurs dans les cases de l'arbre et aussi nous verons comment une condition qui semble compliquée peut être réduite à quelque chose de très simple.
Le problème :
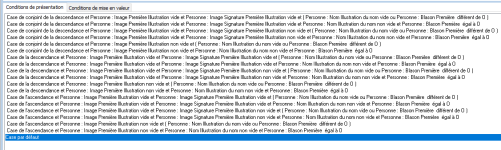
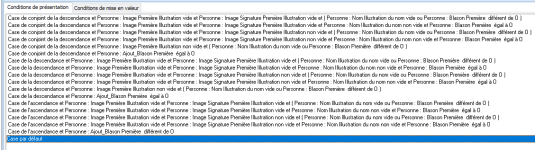
Dans le modèle "mode1-2018.grf" nous voulons modifier la couleur des événements affichés selon les critères suivants :
- L'événement est en caractère noirs si il à une source ET une illustration
- L'événement est en caractères bleus si il a une source OU une illustration mais pas les deux
- L'événement est en rouge si il n'a ni source ni illustration.
Là ou ça se complique c'est que la condition doit pouvoir tenir compte de l'équivalence définie pour les événements, Ainsi, par exemple, on considèrera l'événement complet si le baptême à une source mais pas d'illustration et que la naissance à une illustration et pas de source. Dans ce qui suit nous ne traiterons que l'événement Naissance / Baptême mais le traitement est le même pour les autres événements.
Si l'on ne veut pas oublier de cas, le plus simple est de faire une "Table de vérité" qui décrit tous les cas possibles. Nous adopterons la convention suivante :
- Ni=0 pas d'illustration naissance
- Ni=1 illustration naissance présente
- Ns idem pour source naissance
- Bi ; Bs idem pour illustration et source baptême
Pour la couleur Rouge, c'est très simple ; si on n'a ni illustration ni source pour Naissance ou Baptême on met en rouge :
Ni vide ET Ns vide ET Bi vide ET Bs vide ---> Rouge c'est notre première condition de mise en valeur, sachant qu'au départ les caractère sont noir dans les conditions de présentation.
Pour mettre en bleu, c'est plus compliqué
On peut donc définir notre table de vérité des 16 cas possibles, "So" étant la sortie (1 = bleu)
Ni 0 0 0 0 0 0 0 0 1 1 1 1 1 1 1 1
Ns 0 0 0 0 1 1 1 1 0 0 0 0 1 1 1 1
Bi 0 0 1 1 0 0 0 0 1 1 1 1 0 0 0 0
Bs 0 1 0 1 0 1 0 1 0 1 0 1 0 1 0 1
So 0 1 1 0 1 1 0 0 1 0 1 0 0 0 0 0
Une fois les 4 premières lignes remplies mécaniquement (c'est juste une alternance de 1 et de 0), on regarde pour chaque colonne si la combinaison doit mettre en bleu l'affichage de l'événement Naissance/Baptême ; si oui, on met 1, si non on met 0. Exemple, la deuxième colonne 0001 il n'y a qu'une source au baptême ---> Bleu ---> 1
On voit que on peut avec cette table définir notre condition de mise en valeur qui fera passer la naissance/baptême en couleur bleue, mais c'est très lourd puisqu'il que l'on a 6 combinaisons qui donnent la couleur bleue. La condition sera du genre :
(Ni vide ET Ns vide ET Bi vide ET Bs non vide) OU (Ni vide ET Ns vide ET Bi non vide ET Bs vide) OU (....) OU (....) OU (....) OU (....)
C'est lourd mais tout y est.
Peut-on simplifier cette condition ? OUI, par deux moyens : En utilisant les propriétés de l'algèbre de Bool ou en utilisant la méthode graphique (beaucoup plus simple) de la "Table de Karnaugh". Si par hasard vous avez oublié cette intéressante méthode je conseille fortement la page suivante :
Avec cette méthode, notre table de Karnaugh sera : (en notant a=Ni ; b=Ns ; c=Bi ; d=Bs)

On remarque que la case 00/00 devait être à zéro mais ce cas est traité par la condition de mise en valeur située après (celle qui met en rouge) on peut donc mettre n'importe quelle valeur de sortie pour le cas 00/00. Mettre 1 simplifie l'équation finale obtenue cat il permet de n'avoir que deux groupes de 4.
D'où on déduit (voir la vidéo) la condition simplifiée :
_ _ _ _
a.c+b.d ou encore (Ni vide ET Bi vide) OU (Ns vide ET Bs vide) ce qui est infiniment plus simple que l'équation initiale.
Et dans Généatique on aura la condition pour mettre en bleu Naissance :
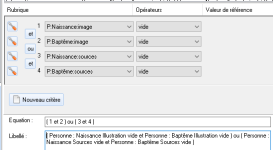
Cette condition n'était pas du tout évidente au départ.
Dans les conditions de mise en valeur on est rarement confronté à des conditions aussi complexes et le simple bon sens suffit généralement à éditer directement les conditions mais souvent on pourrait les simplifier ; ce n'est pas toujours utile et il vaut mieux une condition avec plus de lignes mais qui reste facilement compréhensible. Les simplifications comme celle décrite ici conduisent à des conditions optimales mais pas évidente à interpréter si il faut y revenir.
Le problème :
Dans le modèle "mode1-2018.grf" nous voulons modifier la couleur des événements affichés selon les critères suivants :
- L'événement est en caractère noirs si il à une source ET une illustration
- L'événement est en caractères bleus si il a une source OU une illustration mais pas les deux
- L'événement est en rouge si il n'a ni source ni illustration.
Là ou ça se complique c'est que la condition doit pouvoir tenir compte de l'équivalence définie pour les événements, Ainsi, par exemple, on considèrera l'événement complet si le baptême à une source mais pas d'illustration et que la naissance à une illustration et pas de source. Dans ce qui suit nous ne traiterons que l'événement Naissance / Baptême mais le traitement est le même pour les autres événements.
Si l'on ne veut pas oublier de cas, le plus simple est de faire une "Table de vérité" qui décrit tous les cas possibles. Nous adopterons la convention suivante :
- Ni=0 pas d'illustration naissance
- Ni=1 illustration naissance présente
- Ns idem pour source naissance
- Bi ; Bs idem pour illustration et source baptême
Pour la couleur Rouge, c'est très simple ; si on n'a ni illustration ni source pour Naissance ou Baptême on met en rouge :
Ni vide ET Ns vide ET Bi vide ET Bs vide ---> Rouge c'est notre première condition de mise en valeur, sachant qu'au départ les caractère sont noir dans les conditions de présentation.
Pour mettre en bleu, c'est plus compliqué
On peut donc définir notre table de vérité des 16 cas possibles, "So" étant la sortie (1 = bleu)
Ni 0 0 0 0 0 0 0 0 1 1 1 1 1 1 1 1
Ns 0 0 0 0 1 1 1 1 0 0 0 0 1 1 1 1
Bi 0 0 1 1 0 0 0 0 1 1 1 1 0 0 0 0
Bs 0 1 0 1 0 1 0 1 0 1 0 1 0 1 0 1
So 0 1 1 0 1 1 0 0 1 0 1 0 0 0 0 0
Une fois les 4 premières lignes remplies mécaniquement (c'est juste une alternance de 1 et de 0), on regarde pour chaque colonne si la combinaison doit mettre en bleu l'affichage de l'événement Naissance/Baptême ; si oui, on met 1, si non on met 0. Exemple, la deuxième colonne 0001 il n'y a qu'une source au baptême ---> Bleu ---> 1
On voit que on peut avec cette table définir notre condition de mise en valeur qui fera passer la naissance/baptême en couleur bleue, mais c'est très lourd puisqu'il que l'on a 6 combinaisons qui donnent la couleur bleue. La condition sera du genre :
(Ni vide ET Ns vide ET Bi vide ET Bs non vide) OU (Ni vide ET Ns vide ET Bi non vide ET Bs vide) OU (....) OU (....) OU (....) OU (....)
C'est lourd mais tout y est.
Peut-on simplifier cette condition ? OUI, par deux moyens : En utilisant les propriétés de l'algèbre de Bool ou en utilisant la méthode graphique (beaucoup plus simple) de la "Table de Karnaugh". Si par hasard vous avez oublié cette intéressante méthode je conseille fortement la page suivante :
Avec cette méthode, notre table de Karnaugh sera : (en notant a=Ni ; b=Ns ; c=Bi ; d=Bs)

On remarque que la case 00/00 devait être à zéro mais ce cas est traité par la condition de mise en valeur située après (celle qui met en rouge) on peut donc mettre n'importe quelle valeur de sortie pour le cas 00/00. Mettre 1 simplifie l'équation finale obtenue cat il permet de n'avoir que deux groupes de 4.
D'où on déduit (voir la vidéo) la condition simplifiée :
_ _ _ _
a.c+b.d ou encore (Ni vide ET Bi vide) OU (Ns vide ET Bs vide) ce qui est infiniment plus simple que l'équation initiale.
Et dans Généatique on aura la condition pour mettre en bleu Naissance :

Cette condition n'était pas du tout évidente au départ.
Dans les conditions de mise en valeur on est rarement confronté à des conditions aussi complexes et le simple bon sens suffit généralement à éditer directement les conditions mais souvent on pourrait les simplifier ; ce n'est pas toujours utile et il vaut mieux une condition avec plus de lignes mais qui reste facilement compréhensible. Les simplifications comme celle décrite ici conduisent à des conditions optimales mais pas évidente à interpréter si il faut y revenir.
Dernière édition: